Prove that

To find: formula for h o (g o f)

To prove:

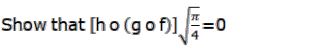
Formula used: $f$ o $f=f(f(x))$

Given: (i) $f: R \rightarrow R: f(x)=x^{2}$

(ii) $g: R \rightarrow R: g(x)=\tan x$

(iii) $h: R \rightarrow R: h(x)=\log x$

Solution: We have,

ho $(g \circ f)=h \circ g(f(x))=h \circ g\left(x^{2}\right)$

$=h\left(g\left(x^{2}\right)\right)=h\left(\tan x^{2}\right)$

$=\log \left(\tan x^{2}\right)$

h o $(g \circ f)=\log \left(\tan x^{2}\right)$

For,  $[h \circ(g \circ f)] \sqrt{\frac{\pi}{4}}$

$=\log \left[\tan \left(\sqrt{\frac{\pi}{4}}\right)^{2}\right]$

$=\log \left[\tan \frac{\pi}{4}\right]$

$=\log 1$

= 0

Hence Proved.