PQRS is a rectangle inscribed in a quadrant

True

Given, PS = 5 cm

radius of circle = SQ = 13 cm

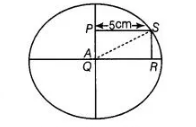
In right angled $\triangle S P Q, \quad S Q^{2}=P Q^{2}+P S^{2} \quad$ [by Pythagoras theorem]

$(13)^{2}=P Q^{2}+(5)^{2}$

$\Rightarrow$ $P Q^{2}=169-25=144$

$\Rightarrow$ $P Q=12 \mathrm{~cm}$

[taking positive square root, because length is always positive]

Now, area of $\triangle A P S=\frac{1}{2} \times$ Base $\times$ Height

$=\frac{1}{2} \times P S \times P Q$

$=\frac{1}{2} \times 5 \times 12=30 \mathrm{~cm}^{2}$

So, given statement is true, if $A$ coincides $Q$.