PQ is a chord of length 4.8 cm of a circle of radius 3 cm.

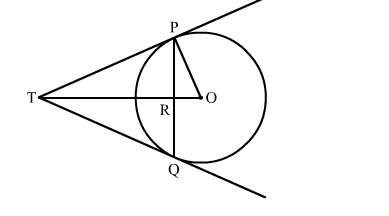
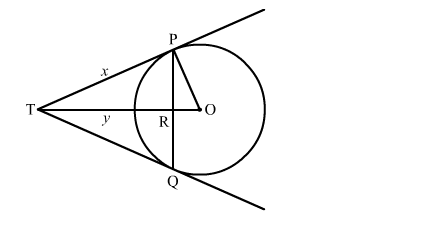
Let TR = y and TP = x
We know that the perpendicular drawn from the centre to the chord bisects it.
∴ PR = RQ
Now, PR + RQ = 4.8
⇒ PR + PR = 4.8
⇒ PR = 2.4
Now, in right triangle POR
By Using Pyhthagoras theorem, we have
PO2 = OR2 + PR2
⇒ 32 = OR2 + (2.4)2
⇒ OR2 = 3.24
⇒ OR = 1.8
Now, in right triangle TPR
By Using Pyhthagoras theorem, we have
TP2 = TR2 + PR2
⇒ x2 = y2 + (2.4)2
⇒ x2 = y2 + 5.76          .....(1)
Again, in right triangle TPQ
By Using Pyhthagoras theorem, we have
TO2 = TP2 + PO2
⇒ (y + 1.8)2 = x2 + 32
⇒ y2 + 3.6y + 3.24 = x2 + 9
⇒ y2 + 3.6y = x2 + 5.76          .....(2)
Solving (1) and (2), we get
x = 4 cm and y = 3.2 cm
∴ TP = 4 cm