PQ is a chord of length 16 cm of a circle of radius 10 cm.

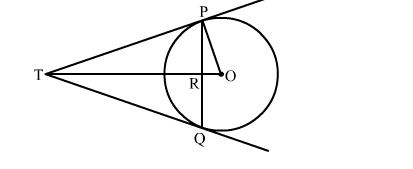
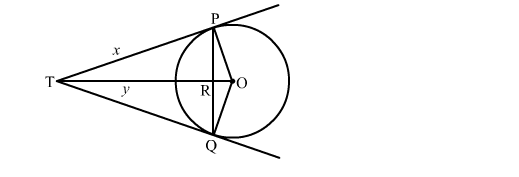
Let TR = y and TP = x
We know that the perpendicular drawn from the centre to the chord bisects it.
∴ PR = RQ
Now, PR + RQ = 16
⇒ PR + PR = 16
⇒ PR = 8
Now, in right triangle POR
By Using Pyhthagoras theorem, we have
PO2 = OR2 + PR2
⇒ 102 = OR2 + (8)2
⇒ OR2 = 36
⇒ OR = 6
Now, in right triangle TPR
By Using Pyhthagoras theorem, we have
TP2 = TR2 + PR2
⇒ x2 = y2 + (8)2
⇒ x2 = y2 + 64          .....(1)
Again, in right triangle TPQ
By Using Pyhthagoras theorem, we have
TO2 = TP2 + PO2
⇒ (y + 6)2 = x2 + 102
⇒ y2 + 12y + 36 = x2 + 100
⇒ y2 + 12y = x2 + 64          .....(2)
Solving (1) and (2), we get
x = 10.67
∴ TP = 10.67 cm