P is any point on the side BC of a ∆ABC. P is joined to A.

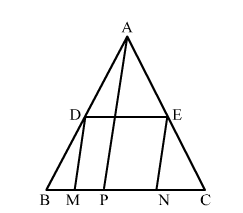
Given: In ∆ABC, M, N, D and E are the mid-points of BP, CP, AB and AC, respectivley.

In ∆ABP,

∵">∵∵ D and M are the mid-points of AB,and BP, respectively.      (Given)

$\therefore B M=\frac{1}{2} A P$ and $B M \| A P$       (Mid-point theorem)       ...(i)

Again, in ∆ACP,

$\because E$ and $N$ are the mid-points of $A C$, and $C P$, respectively.       (Given)

$\therefore E N=\frac{1}{2} A P$ and $E N \| A P$   (Mid-point theorem)       ...(ii)

From (i) and (ii), we get

BM = EN and BM || EN

But this a pair of opposite sides of the quadrilateral DENM.

So, DENM is a parallelgram.

Hence, the correct option is (b).