P is any point on the diagonal AC of a parallelogram ABCD.

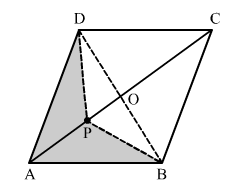
Join BD. 
Let BD and AC intersect at point O. 
O is thus the midpoint of DB and AC. 
PO is the median of △">△DPB, 
So, 

$\operatorname{ar}(\triangle \mathrm{DPO})=\operatorname{ar}(\triangle \mathrm{BPO}) \quad \ldots(1)$

$\operatorname{ar}(\triangle \mathrm{ADO})=\operatorname{ar}(\triangle \mathrm{ABO}) \quad \ldots . .(2)$

Case 1 .

$(2)-(1)$

$\Rightarrow \operatorname{ar}(\triangle \mathrm{ADO})-\operatorname{ar}(\triangle \mathrm{DPO})=\operatorname{ar}(\triangle \mathrm{ABO})-\operatorname{ar}(\triangle \mathrm{BPO})$

Thus, ar(∆ADP) = ar(∆ABP)

Case II: 

$\operatorname{ar}(\triangle \mathrm{ADO})+\operatorname{ar}(\triangle \mathrm{DPO})=\operatorname{ar}(\triangle \mathrm{ABO})+\operatorname{ar}(\triangle \mathrm{BPO})$

Thus, $\operatorname{ar}(\Delta \mathrm{ADP})=\operatorname{ar}(\Delta \mathrm{ABP})$