P and O are points on opposite sides AD and BC of a parallelogram ABCD such that PQ passes through the point of intersection O of its diagonals AC
and BD. Show that PQ is bisected at O.
Thinking Process
Firstly, prove that ΔODP and ΔOBQ are congruent by ASA rule. Further show the required result by CPCT rule
Given $A B C D$ is a parallelogram whose diagonals bisect each other at $O$. To show $P Q$ is bisected at $O$.
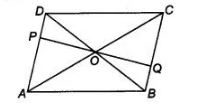
In $\triangle O D P$ and $\triangle O B Q$,
$\angle B O Q=\angle P O D$ [since, vertically opposite angles]
$\angle O B Q=\angle O D P$ [ alternate interior angles]
and $\quad O B=O D \quad$ [given]
$\begin{array}{lll}\therefore & \Delta O D P \cong \Delta O B Q & \text { [by ASA congruence rule ] }\end{array}$
$\therefore \quad O P=O Q$ [by CPCT rule]
So, $P Q$ is bisected at $O$.
Hence proved.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.