One says. "give me hundred, friend! I shall then become twice as rich as you" The other replies,

21. Let the money with first person be Rsx and the money with the second person be Rsy. Then,

$(x+100)=2(y-100)$

$(y+10)=6(x-10)$

If first person gives $R s 100$ to second person then the second person will become twice as rich as first person, According to the given condition, we have,

$(x+100)=2(y-100)$

$x+100=2 y-200$

$x-2 y+100+200=0$

$x-2 y+300=0 \cdots(i)$

if second person gives $R s 10$ to first person then the first person will becomes six times as rich as second person, According to given condition, we have,

$(y+10)=6(x-10)$

$y+10=6 x-60$

$0=6 x-60-y-10$

$0=6 x-y-70 \cdots(i i)$

Multiplying $(i i)$ equation by 2 we get,

$12 x-2 y-140=0 \cdots($ iii $)$

By subtracting $(i i i)$ from $(i)$, we get

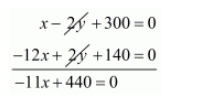
$-11 x=-440$

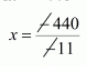
$x=40$

Putting $x=40$ in equation $(i)$, we get,

$x-2 y+300=0$

$40-2 y+300=0$

$-2 y+340=0$

$-2 y=-340$

$y=170$

Hence, first person's capital will be $R s, 40$,

Second person's capital will be $R s .170$.