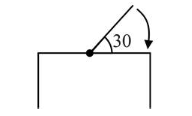
One end of a straight uniform $1 \mathrm{~m}$ long bar is pivoted on horizontal table. It is released from rest when it makes an angle $30^{\circ}$ from the horizontal (see figure). Its angular speed when it hits the table is given as $\sqrt{n} s^{-1}$, where $n$ is an integer. The value of $n$ is_____
(15) Here, length of bar, $\mathrm{l}=1 \mathrm{~m}$
angle, $\theta=30^{\circ}$
$\Delta P E=\Delta K E$ or $m g h=\frac{1}{2} I \omega^{2}$
$\Rightarrow(\mathrm{mg}) \frac{l}{2} \sin 30^{\circ}=\frac{1}{2}\left(\frac{m l^{2}}{3}\right) \omega^{2}$
$\Rightarrow \mathrm{mg} \frac{l}{2} \times \frac{1}{2}=\frac{1}{2}\left(\frac{m l^{2}}{3}\right) \omega^{2}$
$\Rightarrow \omega=\sqrt{15} \mathrm{rad} / \mathrm{s}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.