On the same side of a tower, two objects are located.

Let AB be the tower of height m and Two objects are located when top of tower are observed, makes an angle of depression from the top and bottom of tower are  and  respectively.

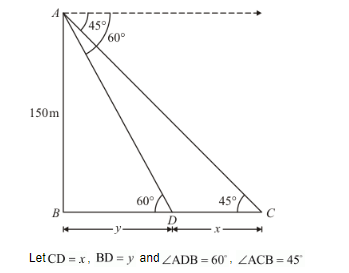
So we use trigonometric ratios.

In a triangle ABC,

$\tan 45^{\prime}=\frac{150}{x+y}$

$\Rightarrow x+y=150$ ............(1)

Again in a triangle ABD,

$\tan 60^{\circ}=\frac{150}{y}$

$\Rightarrow \sqrt{3}=\frac{150}{y}$]

$\Rightarrow \sqrt{3} y=150$ ........(2)

So from (1) and (2) we get

$x+\frac{150}{\sqrt{3}}=150$

$\Rightarrow \sqrt{3} x=150(\sqrt{3}-1)$

$\Rightarrow x=63.39$

Hence the required distance is approximately  m.