On a horizontal plane there is a vertical tower with a flagpole on the top of the tower.

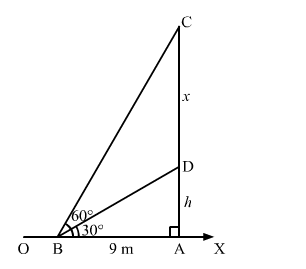
Let $O X$ be the horizontal plane, $A D$ be the tower and $C D$ be the vertical flagpole.

We have:

$A B=9 \mathrm{~m}, \angle D B A=30^{\circ}$ and $\angle C B A=60^{\circ}$

Let:

$A D=h \mathrm{~m}$ and $C D=x \mathrm{~m}$

In the right $\triangle A B D$, we have:

$\frac{A D}{A B}=\tan 30^{\circ}=\frac{1}{\sqrt{3}}$

$\Rightarrow \frac{h}{9}=\frac{1}{\sqrt{3}}$

$\Rightarrow h=\frac{9}{\sqrt{3}}=5.19 \mathrm{~m}$

Now, in the right $\triangle A B C$, we have:

$\frac{A C}{B A}=\tan 60^{\circ}=\sqrt{3}$

$\Rightarrow \frac{h+x}{9}=\sqrt{3}$

$\Rightarrow h+x=9 \sqrt{3}$

By putting $h=\frac{9}{\sqrt{3}}$ in the above equation, we get:

$\frac{9}{\sqrt{3}}+x=9 \sqrt{3}$

$\Rightarrow x=9 \sqrt{3}-\frac{9}{\sqrt{3}}$

$\Rightarrow x=\frac{27-9}{\sqrt{3}}=\frac{18}{\sqrt{3}}=\frac{18}{1.73}=10.4$

Thus, we have:
Height of the flagpole = 10.4 m
Height of the tower = 5.19 m