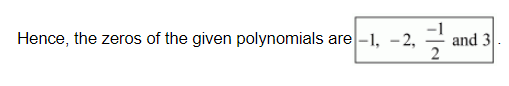Obtain all zeros of the polynomial f(x) = 2x4 + x3 − 14x2 − 19x − 6, if two of its zeros are −2 and −1.

We know that, if $x=\alpha$ is a zero of a polynomial, and then $x-\alpha$ is a factor of $f(x)$

Since $_{-2}$ and $_{-1}$ are zeros of $f(x)$.

Therefore 

$(x+2)(x+1)=x^{2}+2 x+x+2$

$=x^{2}+3 x+2$

$x^{2}+3 x+2$ is a factor of $f(x)$. Now, We divide $2 x^{4}+x^{3}-14 x^{2}-19 x-6$ by $g(x)=x^{2}+3 x+2$ to find the other zeros of $f(x)$.

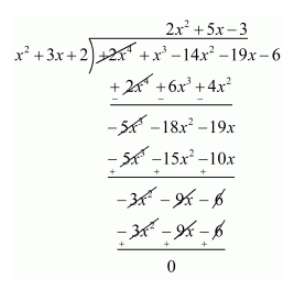
By using division algorithm we have, $f(x)=g(x) \times q(x)-r(x)$

$2 x^{4}+x^{3}-14 x^{2}-19-6=\left(x^{2}+3 x+2\right)\left(2 x^{2}-5 x-3\right)$

$2 x^{4}+x^{3}-14 x^{2}-19-6=\left(x^{2}+2 x+1 x+2\right)\left(2 x^{2}-6 x+1 x-3\right)$

$2 x^{4}+x^{3}-14 x^{2}-19-6=[x(x+2)+1(x+2)][2 x(x-3)+1(x-3)]$

$2 x^{4}+x^{3}-14 x^{2}-19-6=[(x+1)(x+2)(2 x+1)(x-3)]$