Question:
Observe the following pattern:
13 = 1
13 + 23 = (1 + 2)2
13 + 23 + 33 = (1 + 2 + 3)2
Write the next three rows and calculate the value of 13 + 23 + 33 + ... + 93 + 103 by the above pattern.
Solution:
Extend the pattern as follows:
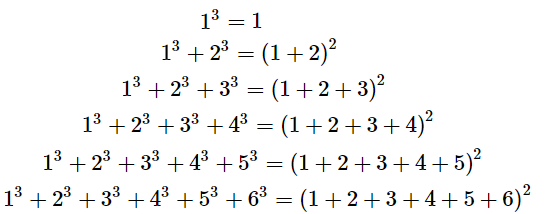
Now, from the above pattern, the required value is given by:
$1^{3}+2^{3}+3^{3}+4^{3}+5^{3}+6^{3}+7^{3}+8^{3}+9^{3}+10^{3}=(1+2+3+4+5+6+7+8+9+10)^{2}=55^{2}$
= 3025
Thus, the required value is 3025 .
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.