Question:
OACB is a quadrant of a circle with centre O and its radius is 3.5 cm. If OD = 2 cm.
find the area of
(i) quadrant OACB
(ii) the shaded region.
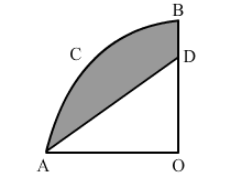
Solution:
(i) Area of the quadrant $O A C B=\left(\frac{1}{4} \times \frac{22}{7} \times 3.5 \times 3.5\right) \mathrm{cm}^{2}$
$=\left(\frac{1}{4} \times \frac{22}{7} \times \frac{35}{10} \times \frac{35}{10}\right) \mathrm{cm}^{2}$
$=\frac{77}{8} \mathrm{~cm}^{2}$
$=9.625 \mathrm{~cm}^{2}$
(ii) Area of the shaded region = Area of the quadrant $O A C B$ - Area of $\triangle A O D$
$=\left|\left(\frac{77}{8}\right)-\left(\frac{1}{2} \times 3.5 \times 2\right)\right| \mathrm{cm}^{2}$
$=\left(\frac{77}{8}-\frac{35}{10}\right) \mathrm{cm}^{2}$
$=\frac{49}{8} \mathrm{~cm}^{2}$
$=6.125 \mathrm{~cm}^{2}$
