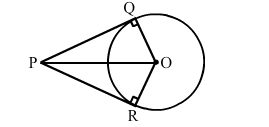
O is the centre of a circle of radius 5 cm. At a distance of 13 cm from O, a point P is taken.

(a) 60 cm2

Given,

$O Q=O R=5 \mathrm{~cm}, O P=13 \mathrm{~cm} .$

$\angle O Q P=\angle O R P=90^{\circ}$ (T angents drawn from an external point are perpendicular

to the radius at the point of contact)

From right - angled $\triangle P O Q$ :

$P Q^{2}=\left(O P^{2}-O Q^{2}\right)$

$\Rightarrow P Q^{2}=13^{2}-5^{2}$

$\Rightarrow P Q^{2}=169-25$

$\Rightarrow P Q^{2}=144$

$\Rightarrow P Q=\sqrt{144}$

$\Rightarrow P Q=12 \mathrm{~cm}$

$\therefore a r(\triangle O Q P)=\frac{1}{2} \times P Q \times O Q$

$\Rightarrow a r(\triangle O Q P)=\left(\frac{1}{2} \times 12 \times 5\right) \mathrm{cm}^{2}$

$\Rightarrow \operatorname{ar}(\triangle O Q P)=30 \mathrm{~cm}^{2}$

Similarly, $a r(\triangle O R P)=30 \mathrm{~cm}^{2}$

$\therefore \operatorname{ar}($ quad. PQOR $)=(30+30) \mathrm{cm}^{2}=60 \mathrm{~cm}^{2}$