O is a point in the interior of a square ABCD

Given $O$ is a point in the interior of a square $A B C D$ such that $\triangle O A B$ is an equilateral triangle.

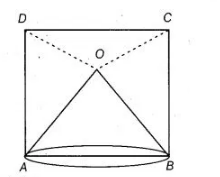
Construction Join $O C$ and $O D$.

To show $\triangle O C D$ is an isosceles triangle.

Proof Since, $A O B$ is an equilateral triangle.

$\therefore \quad \angle O A B=\angle O B A=60^{\circ}$ $\ldots(i)$

Also, $\angle D A B=\angle C B A=90^{\circ}$   ......(ii) [each angle of a square is $90^{\circ}$ ]

$[\because A B C D$ is a square $]$

On subtracting Eq. (i) from Eq. (ii), we get

$\angle D A B-\angle O A B=\angle C B A-\angle O B A=90^{\circ}-60^{\circ}$

i.e., $\angle D A O=\angle C B O=30^{\circ}$

In $\triangle A O D$ and $\triangle B O C$,

$A O=B O$ [given]

[all the side of an equilateral triangle are equal]

$\angle D A O=\angle C B O \quad$ [proved above]

and $\quad A D=B C \quad$ [sides of a square are equal]

$\begin{array}{lll}\therefore & \Delta A O D \equiv \triangle B O C & \text { [by SAS congruence rule] }\end{array}$

Hence, $O D=O C$ [by CPCT]

In $\triangle C O D$, 

$O C=O D$

Hence, $\triangle C O D$ is an isosceles triangle.

Hence proved.