Question:
Two circuits are shown in the figure (a) \& (b). At a frequency of $\mathrm{rad} / \mathrm{s}$ the average power dissipated in one cycle will be same in both the circuits.
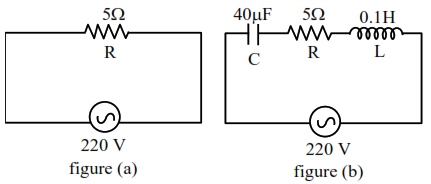
Solution:
For figure (a)
$P_{\text {avg }}=\frac{v_{\mathrm{rms}}^{2}}{R}$
$\frac{\mathrm{v}_{\mathrm{rms}}^{2}}{\mathrm{Z}^{2}} \times \mathrm{R}=\frac{\mathrm{v}_{\mathrm{rms}}^{2}}{\mathrm{R}} \times 1$
$\mathrm{R}^{2}=\mathrm{Z}^{2}$
$25=\left(\sqrt{\left(\mathrm{x}_{\mathrm{C}}-\mathrm{x}_{\mathrm{L}}\right)^{2}+5^{2}}\right)^{2}$
$25=\left(\mathrm{x}_{\mathrm{c}}-\mathrm{x}_{\mathrm{L}}\right)^{2}+25$
$\mathrm{x}_{\mathrm{c}}=\mathrm{x}_{\mathrm{L}} \Rightarrow \frac{1}{\omega \mathrm{C}}=\omega \mathrm{L}$
$\omega^{2}=\frac{1}{\mathrm{LC}}=\frac{10^{6}}{0.1 \times 40}$
$\omega=500$
