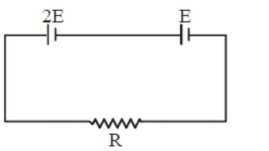
Two cells of emf $2 \mathrm{E}$ and $\mathrm{E}$ with internal resistance $\mathrm{r}_{1}$ and $\mathrm{r}_{2}$ respectively are connected in series to an external resistor $R$ (see figure). The value of $\mathrm{R}$, at which the potential difference across the terminals of the first cell becomes zero is
Correct Option: 2,
(2)
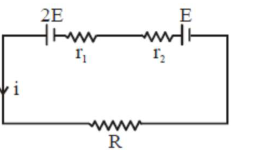
$\mathrm{i}=\frac{3 \mathrm{E}}{\mathrm{R}+\mathrm{r}_{1}+\mathrm{r}_{2}}$
$\mathrm{TPD}=2 \mathrm{E}-\mathrm{ir}_{1}=0$
$2 \mathrm{E}=\mathrm{ir}_{1}$
$2 \mathrm{E}=\frac{3 \mathrm{E} \times \mathrm{r}_{1}}{\mathrm{R}+\mathrm{r}_{1}+\mathrm{r}_{2}}$
$2 \mathrm{R}+2 \mathrm{r}_{1}+2 \mathrm{r}_{2}=3 \mathrm{r}_{1}$
$\mathrm{R}=\frac{\mathrm{r}_{1}}{2}-\mathrm{r}_{2}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.