Solve this following

$|x|+|y| \leq 1$

$2 y^{2} \geq|x|$

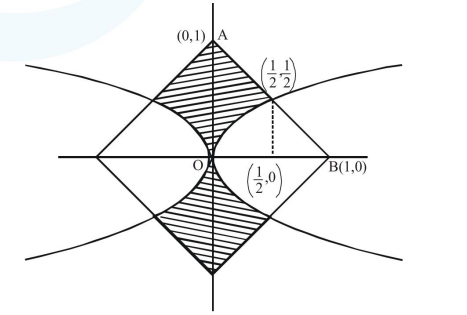
For point of intersection

$x+y=1 \Rightarrow x=1-y$

$\mathrm{y}^{2}=\frac{\mathrm{x}}{2} \Rightarrow 2 \mathrm{y}^{2}=\mathrm{x}$

$2 \mathrm{y}^{2}=1-\mathrm{y} \Rightarrow 2 \mathrm{y}^{2}+\mathrm{y}-1=0$

$(2 \mathrm{y}-1)(\mathrm{y}+1)=0$

$y=\frac{1}{2}$ or $-1$

Now Area of $\Delta \mathrm{OAB}=\frac{1}{2} \times 1 \times 1=\frac{1}{2}$

Area of Region $\mathrm{R}_{1}=\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}=\frac{1}{8}$

Area of Region $\mathrm{R}_{2}=\frac{1}{\sqrt{2}} \int_{0}^{\frac{1}{2}} \sqrt{\mathrm{x}} \mathrm{dx}=\frac{1}{6}$

Now area of shaded region in first quadrant

$=$ Area of $\Delta \mathrm{OAB}-\mathrm{R}_{1}-\mathrm{R}_{2}$

$=\frac{1}{2}-\left(\frac{1}{6}\right)-\left(\frac{1}{8}\right)=\frac{5}{24}$

So required area $=4\left(\frac{5}{24}\right)=\frac{5}{6}$

so option (4) is correct.