Question:
Minimise and Maximise $Z=x+2 y$
subject to $x+2 y \geq 100,2 x-y \leq 0,2 x+y \leq 200 ; x, y \geq 0$.
Solution:
The feasible region determined by the constraints, x + 2y ≥ 100, 2x − y ≤ 0, 2x + y ≤ 200, x ≥ 0, and y ≥ 0, is as follows.
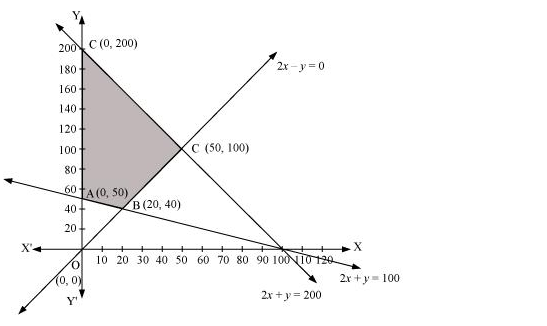
The corner points of the feasible region are A(0, 50), B(20, 40), C(50, 100), and D(0, 200).
The values of Z at these corner points are as follows.
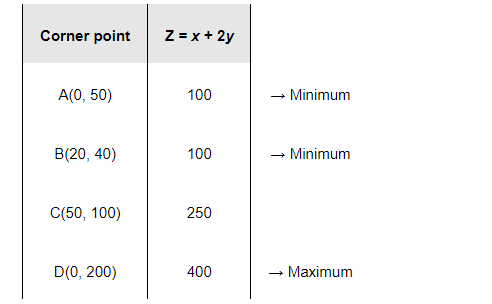
The maximum value of Z is 400 at (0, 200) and the minimum value of Z is 100 at all the points on the line segment joining the points (0, 50) and (20, 40).
