Question:
Meena went to a bank to withdraw Rs 2000. She asked the cashier to give her Rs 50 and Rs 100 notes only. Meena got 25 notes in all. Find how many notes Rs 50 and Rs 100 she received.
Solution:
Let $R s . x$ be the notes of $R s .50$ and $R s .100$ notes will be $R s . y$
If Meena ask for $R s .50$ and $R s .100$ notes only, then the equation will be,
$50 x+100 y=2000$
Divide both sides by 50 then we get,
$x+2 y=40 \cdots(i)$
If Meena got 25 notes in all then the equation will be,
$x+y=25 \cdots(i i)$
By subtracting the equation $(i i)$ from $(i)$ we get,
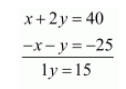
$y=\frac{15}{1}$
$y=15$
Substituting $y=15$ in equation $(i i)$, we get
$x+y=25$
$x+15=25$
$x=25-15$
$x=10$
Therefore $x=10$ and $y=15$
Hence, Meena has 10 notes of $R s .50$ and 15 notes of $R s .100$
