Question:
Maximise $Z=-x+2 y$, subject to the constraints:
$x \geq 3, x+y \geq 5, x+2 y \geq 6, y \geq 0$
Solution:
The feasible region determined by the constraints, $x \geq 3, x+y \geq 5, x+2 y \geq 6$, and $y \geq 0$, is as follows.
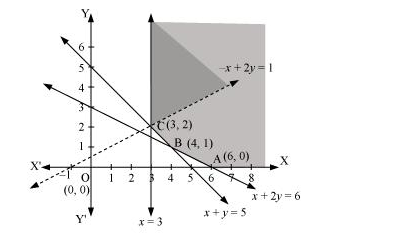
It can be seen that the feasible region is unbounded.
The values of Z at corner points A (6, 0), B (4, 1), and C (3, 2) are as follows.

As the feasible region is unbounded, therefore, Z = 1 may or may not be the maximum value.
For this, we graph the inequality, −x + 2y > 1, and check whether the resulting half plane has points in common with the feasible region or not.
The resulting feasible region has points in common with the feasible region.
Therefore, Z = 1 is not the maximum value. Z has no maximum value.
