Match the following columns:

(a) - (r)
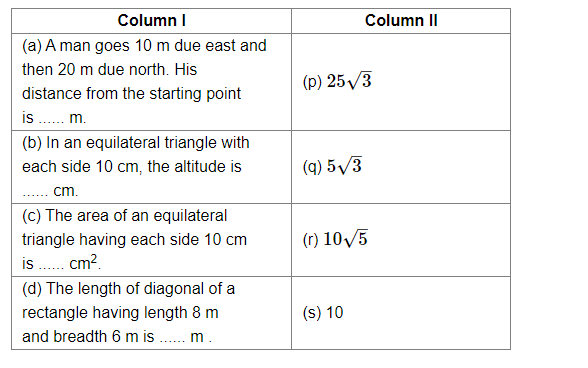
Let the man starts from A and goes 10 m due east at B and then 20 m due north at C.
Then, in right-angled triangle ABC, we have:

$A B^{2}+B C^{2}=A C^{2}$

$\Rightarrow A C=\sqrt{10^{2}+20^{2}}=\sqrt{100+200}=10 \sqrt{3}$

Hence, the man is $10 \sqrt{3} \mathrm{~m}$ away from the starting point.

(b) - (q)
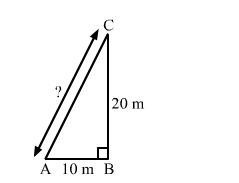
Let the triangle be ABC with altitude AD.
In right-angled triangle ABD, we have:

$A B^{2}=A D^{2}+B D^{2}$

$\Rightarrow A D^{2}=10^{2}-5^{2} \quad\left(\because B D=\frac{1}{2} B C\right)$

$\Rightarrow A D=\sqrt{100-25}=\sqrt{75}=5 \sqrt{3} \mathrm{~cm}$

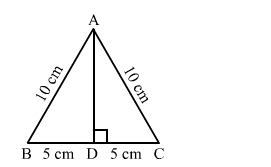
(c) - (p)

Area of an equilateral triangle with side $a=\frac{\sqrt{3}}{4} a^{2}=\frac{\sqrt{3}}{4} \times 10^{2}=\sqrt{3} \times 5 \times 5$

$=25 \sqrt{3} \mathrm{~cm}^{2}$

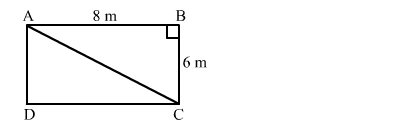
(d) - (s)
Let the rectangle be ABCD with diagonals AC and BD.
In right-angled triangle ABC, we have:

$A C^{2}=A B^{2}+B C^{2}=8^{2}+6^{2}=64+36$

$\Rightarrow A C=\sqrt{100}=10 \mathrm{~m}$