M and N are points on opposite sides AD and BC of a parallelogram ABCD such that MN passes through the point of intersection O

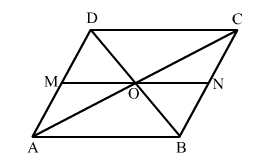
Given: A parallelogram ABCD
 
To prove: MN is bisected at O

Proof:

In  ∆">Δ∆OAM and ∆">Δ∆OCN,

OA = OC                 (Diagonals of parallelogram bisect each other)

∠AOM = ∠CON      (Vertically opposite angles)

∠MAO = ∠OCN       (Alternate interior angles)

∴">∴∴ By ASA congruence criteria,

$\Delta O A M \cong \Delta O C N$

$\Rightarrow O M=O N(\mathrm{CPCT})$

Hence, MN is bisected at O.