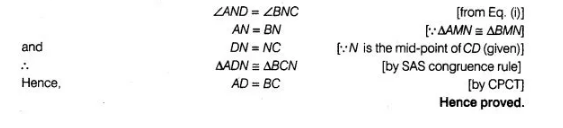Question:
Line segment joining the mid-points M and N of parallel sides AB and DC, respectively of a trapezium ABCD is perpendicular to both the sides AB and DC. Prove that AD = BC.
Solution:
Given In trapezium $A B C D$, points $M$ and $N$ are the mid-points of parallel sides $A B$ and $D C$ respectively and join $M N$, which is perpendicular to $A B$ and $D C$.
To prove
$A D=B C$
Proof Since, $M$ is the mid-point of $A B$.

On multiplying both sides of above equation by $-1$ and than adding $90^{\circ}$ both sides, we get
$90^{\circ}-\angle 1=90^{\circ}-\angle 2$
$\Rightarrow \quad \angle A N D=\angle B N C$ ...(i)

Now, in $\triangle A D N$ and $\triangle B C N$,