Let X be a random variable with distribution.

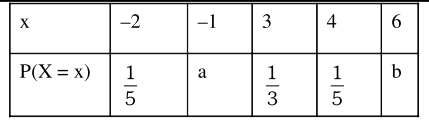
$\bar{X}=2.3$.

$-a+6 b=\frac{9}{10}$..(1)

$\sum P_{i}=\frac{1}{5}+a+\frac{1}{3}+\frac{1}{5}+b=1$

$a+b=\frac{4}{15}$..(2)

From equation (1) and (2)

$a=\frac{1}{10}, \quad b=\frac{1}{6}$

$\sigma^{2}=\Sigma p_{i} x_{i}^{2}-(\bar{X})^{2}$

$\frac{1}{5}(4)+a(1)+\frac{1}{3}(9)+\frac{1}{5}(16)+b(36)-(2.3)^{2}$

$=\frac{4}{5}+a+3+\frac{16}{5}+36 b-(2.3)^{2}$

$=4+a+3+36 b-(2.3)^{2}$

$=7+a+36 b-(2.3)^{2}$

$=7+\frac{1}{10}+6-(2.3)^{2}$

$=13+\frac{1}{10}-\left(\frac{23}{10}\right)^{2}$

$=\frac{131}{10}-\left(\frac{23}{10}\right)^{2}$

$=\frac{1310-(23)^{2}}{100}$

$=\frac{1310-529}{100}$

$\sigma^{2}=\frac{781}{100}$

$100 \sigma^{2}=781$