Let the tangent to the parabola $\mathrm{S}: \mathrm{y}^{2}=2 \mathrm{x}$ at the point $\mathrm{P}(2,2)$ meet the $\mathrm{X}$-axis at $\mathrm{Q}$ and normal at it meet the parabola $S$ at the point $R$. Then the area (in sq. units) of the triangle PQR is equal to:
Correct Option: 1
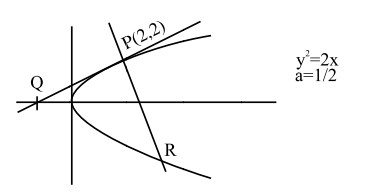
Tangent at $\mathrm{P}: \mathrm{y}(2)=2(1 / 2)(\mathrm{x}+2)$
$\Rightarrow 2 y=x+2$
$\therefore Q=(-2,0)$
Normal at $\mathrm{P}: \mathrm{y}-2=-\frac{(2)}{2 \cdot 1 / 2}(\mathrm{x}-2)$
$\Rightarrow \mathrm{y}-2=-2(\mathrm{x}-2)$
$\Rightarrow \mathrm{y}=6-2 \mathrm{x}$
$\therefore$ Solving with $y^{2}=2 x \Rightarrow R\left(\frac{9}{2}-3\right)$
$\therefore \operatorname{Ar}(\Delta \mathrm{PQR})=\frac{1}{2}\left|\begin{array}{ccc}2 & 2 & 1 \\ -2 & 1 & 1 \\ \frac{9}{2} & 3- & 1\end{array}\right|$
$=\frac{25}{2}$ sq.units
