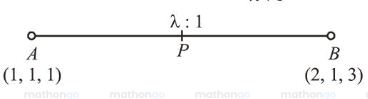
Let the position vectors of points 'A' and 'B' be

Let position vector of $A$ and $B$ be $\vec{a}$ and $\vec{b}$ respectively.

$\therefore$ Position vector of $P$ is $\overrightarrow{O P}=\frac{\lambda \vec{b}+\vec{a}}{\lambda+1}$

Given $\overrightarrow{O B} \cdot \overrightarrow{O P}-3|\overrightarrow{O A} \times \overrightarrow{O P}|^{2}=6$

$\Rightarrow \vec{b} \cdot\left(\frac{\lambda \vec{b}+\vec{a}}{\lambda+1}\right)-3\left|\vec{a} \times \frac{\lambda \vec{b}+\vec{a}}{\lambda+1}\right|^{2}=6$

$\Rightarrow \frac{\vec{a} \cdot \vec{b}+\lambda|\vec{b}|^{2}}{\lambda+1}-\frac{3 \lambda^{2}}{(\lambda+1)^{2}}|\vec{a} \times \vec{b}|^{2}=6$

$(\because \vec{a} \times \vec{b}=2 \hat{i}-\hat{j}-\hat{k}$ and $\vec{a} \cdot \vec{b}=6)$

$\Rightarrow \frac{6+14 \lambda}{\lambda+1}-\frac{18 \lambda^{2}}{(\lambda+1)^{2}}=6 \Rightarrow 6+\frac{8 \lambda}{\lambda+1}-\frac{18 \lambda^{2}}{(\lambda+1)^{2}}=6$

Let $\frac{\lambda}{\lambda+1}=t$

\Rightarrow 18 t^{2}-8 t=0 \Rightarrow 2 t(9 t-4)=0

$\Rightarrow t=0, \frac{4}{9}$

$\therefore \frac{\lambda}{\lambda+1}=\frac{4}{9} \Rightarrow \lambda=\frac{4}{5}=0.8$