Question:
Let the mirror image of the point $(1,3$, a) with respect to the plane $\overrightarrow{\mathrm{r}} \cdot(2 \hat{\mathrm{i}}-\hat{\mathrm{j}}+\hat{\mathrm{k}})-\mathrm{b}=0$ be $(-3,5,2)$. Then the value of $|a+b|$ is equal to
Solution:
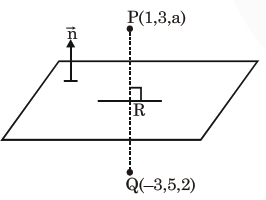
plane $=2 x-y+z=b$
$\mathrm{R} \equiv\left(-1,4, \frac{\mathrm{a}+2}{2}\right) \rightarrow$ on plane
$\therefore-2-4+\frac{\mathrm{a}+2}{2}=\mathrm{b}$
$\Rightarrow a+2=2 b+12 \Rightarrow a=2 b+10 \ldots$ (i)
$<\mathrm{PQ}>=\langle 4,-2, \mathrm{a}-2\rangle$
$\therefore \frac{2}{4}=\frac{-1}{-2}=\frac{1}{a-2}$
$\Rightarrow a-2=2 \Rightarrow a=4, b=-3$
$\therefore|a+b|=1$
