Let the foot of perpendicular from a point $\mathrm{P}(1,2,-1)$ to the straight line $\mathrm{L}: \frac{\mathrm{x}}{1}=\frac{\mathrm{y}}{0}=\frac{\mathrm{z}}{-1}$ be $\mathrm{N}$.
Let a line be drawn from $P$ parallel to the plane $x+y+2 z=0$ which meets $L$ at point $Q$. If $\alpha$ is the acute angle between the lines $\mathrm{PN}$ and $\mathrm{PQ}$, then $\cos \alpha$ is equal to_________.
Correct Option: , 3

$\overrightarrow{P N} \cdot(\hat{i}-\hat{k})=0$
$\Rightarrow \mathrm{N}(1,0,-1)$
Now,
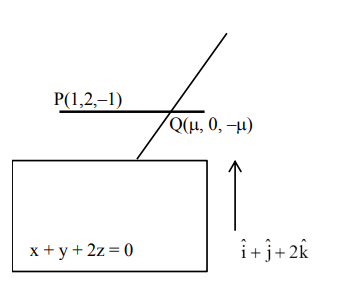
$\overrightarrow{\mathrm{PQ}} \cdot(\hat{\mathrm{i}}+\hat{\mathrm{j}}+2 \hat{\mathrm{k}})=0$
$\Rightarrow \mu=-1$
$\Rightarrow Q(-1,0,1)$
$\overrightarrow{\mathrm{PN}}=2 \hat{\mathrm{j}}$ and $\overrightarrow{\mathrm{PQ}}=2 \hat{\mathrm{i}}+2 \hat{\mathrm{j}}-2 \hat{\mathrm{k}}$
$\Rightarrow \cos \alpha=\frac{1}{\sqrt{3}}$
