Let [t] denote the greatest integer less than or equal

Question:

Let [t] denote the greatest integer less than or equal to $t$. Let $f(x)=x-[x], g(x)=1-x+[x]$, and $h(x)=\min \{f(x), g(x)\}, x \in[-2,2] .$ Then $h$ is :

  1. continuous in $[-2,2]$ but not differentiable at more than four points in $(-2,2)$

  2. not continuous at exactly three points in $[-2,2]$

  3. continuous in $[-2,2]$ but not differentiable at exactly three points in $(-2,2)$

  4. continuous in $[-2,2]$ but not differentiable at exactly three points in $(-2,2)$

Correct Option: 1,

Solution:

$\min \{x-[x], 1-x+[x]\}$

$h(x)=\min \{x-[x], 1-[x-[x])\}$

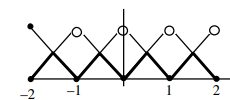
$\Rightarrow \quad$ always continuous in $[-2,2]$

but non differentiable at 7 Points

Leave a comment

eSaral Gurukul

NEET

JEE Main

JEE Advanced

Our Telegram Channel

All Study Material