Let $T$ be the tangent to the ellipse $E: x^{2}+4 y^{2}=5$ at the point $\mathrm{P}(1,1)$. If the area of the region bounded by the tangent $\mathrm{T}$, ellipse $\mathrm{E}$, lines $\mathrm{x}=1$ and $\mathrm{x}=\sqrt{5}$ is $\alpha \sqrt{5}+\beta+\gamma \cos ^{-1}\left(\frac{1}{\sqrt{5}}\right)$, then $|\alpha+\beta+\gamma|$ is equal to
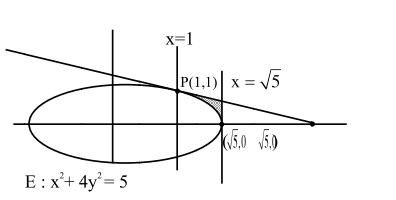
Tangent at $\mathrm{P}: \mathrm{x}+4 \mathrm{y}=5$
Required Area
$=\int_{1}^{\sqrt{5}}\left(\frac{5-x}{4}-\frac{\sqrt{5-x^{2}}}{2}\right) \mathrm{dx}$
$=\left[\frac{5 x}{4}-\frac{x^{2}}{8}-\frac{x}{4} \sqrt{5-x^{2}}-\frac{5}{2} \sin ^{-1} \frac{x}{\sqrt{5}}\right]_{1}^{\sqrt{5}}$
$=\frac{5}{4} \sqrt{5}-\frac{5}{4}-\frac{5}{4} \cos ^{-1}\left(\frac{1}{\sqrt{5}}\right)$
It we assume $\alpha, \beta, \gamma, \in Q$ (Not given in question) then $\alpha=\frac{5}{4}, \beta=-\frac{5}{4} \& \gamma=-\frac{5}{4}$
$|\alpha+\beta+\gamma|=1.25$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.