Let s denotes the semi-perimeter

Solution:

A circle is inscribed in the A ABC, which touches the BC, CA and AB.

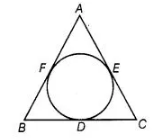
Given, $\quad B C=a, C A=b$ and $A B=c$

By using the property, tangents are drawn from an external point to the circle are equal in length.

$\therefore \quad B D=B F=x \quad$ [say]

$D C=C E=y$ [say]

and $A E=A F=Z$ [say]

NOW, $B C+C A+A B=a+b+c$

$\Rightarrow \quad(B D+D C)+(C E+E A)+(A F+F B)=a+b+c$

$\Rightarrow \quad(x+y)+(y+z)+(z+x)=a+b+c$

$\Rightarrow \quad 2(x+y+z)=2 s$

$[\because 2 s=a+b+c=$ perimeter of $\triangle A B C]$

$\Rightarrow$$s=x+y+z$

$\Rightarrow \quad x=s-(y+z)$

$\Rightarrow \quad B D=s-b$ $[\because b=A E+E C=z+y]$

Hence proved.