Question:
Let $\mathrm{P}(4,-4)$ and $\mathrm{Q}(9,6)$ be two points on the parabola, $y^{2}=4 x$ and let $X$ be any point on the arc POQ of this parabola, where $\mathrm{O}$ is the vertex of this parabola, such that the area of $\triangle \mathrm{PXQ}$ is maximum. Then this maximum area (in sq. units) is :
Correct Option: 1
Solution:
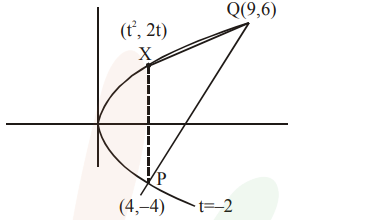
$y^{2}=4 x$
$2 y^{\prime}=4$
$\mathrm{y}^{\prime}=\frac{1}{\mathrm{t}}=2, \mathrm{t}=\frac{1}{2}$
Area $=\frac{1}{2}\left|\begin{array}{ccc}\frac{1}{4} & 1 & 1 \\ 9 & 6 & 1 \\ 4 & -4 & 1\end{array}\right|=\frac{125}{4}$
