Let in a right angled triangle, the smallest angle be
$\theta$. If a triangle formed by taking the reciprocal of its sides is also a right angled triangle, then $\sin \theta$ is equal to :
Correct Option: , 2
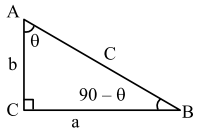
$<\mathrm{A}=\theta$
$<\mathrm{B}=90-\theta$
$a=$ smallest side
$\mathrm{c}^{2}=\mathrm{a}^{2}+\mathrm{b}^{2}$
$\frac{1}{a^{2}}=\frac{1}{b^{2}}+\frac{1}{c^{2}}$
$\frac{\mathrm{b}^{2} \mathrm{c}^{2}}{\mathrm{a}^{2}}=\mathrm{b}^{2}+\mathrm{c}^{2}$
Use $a=2 R \sin A=2 R \sin \theta$
$b=2 R \sin B=2 R \sin (90-\theta)=2 R \cos \theta$
$c=2 R \sin C=2 \sin 90^{\circ}=2 R$
$\frac{4 \mathrm{R}^{2} \cos ^{2} \theta}{4 \mathrm{R}^{2} \sin ^{2} \theta}=4 \mathrm{R}^{2} \cos ^{2} \theta+4 \mathrm{R}^{2}$
$\cos ^{2} \theta=\sin ^{2} \theta \cos ^{2} \theta+\sin ^{2} \theta$
$1-\sin ^{2} \theta=\sin ^{2} \theta\left(1-\sin ^{2} \theta\right)+\sin ^{2} \theta$
$\sin ^{2} \theta=\frac{3-\sqrt{5}}{2}$
$\Rightarrow \sin \theta=\frac{\sqrt{5}-1}{2}$
