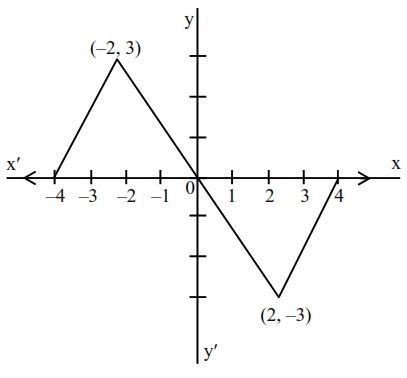Let $f: \mathbf{R} \rightarrow \mathbf{R}$ be a function defined as
$f(x)=\left\{\begin{array}{cl}3\left(1-\frac{|x|}{2}\right) & \text { if } \quad|x| \leq 2 \\ 0 & \text { if } \quad|x|>2\end{array}\right.$
Let $g: \mathbf{R} \rightarrow \mathbf{R}$ be given by $g(x)=f(x+2)-f(x-2)$
If $\mathrm{n}$ and $\mathrm{m}$ denote the number of points in $\mathbf{R}$ where $g$ is not continuous and not differentiable, respectively, then $\mathrm{n}+\mathrm{m}$ is equal to
$f(x-2) \begin{cases}\frac{3 x}{2} & -4 \leq x \leq-2 \\ -\frac{3 x}{2} & -2 $f(x-2) \begin{cases}\frac{3 x}{2} & 0 \leq x \leq 2 \\ -\frac{3 x}{2}+6 & 2 \leq x \leq 4 \\ 0 & x \in(-\infty, 0) \cup(4,+\infty)\end{cases}$ $g(x)=f(x+2)-f(x-2) \begin{cases}\frac{3 x}{2}+6 & -4 \leq x \leq-2 \\ -\frac{3 x}{2} & -2 $\mathrm{n}=0$ $\mathrm{m}=4 \Rightarrow(\mathrm{n}+\mathrm{m}=4)$