Let C be the set of all complex numbers. Let
$\mathrm{S}_{1}=\left\{\mathrm{z} \in \mathrm{C}|| \mathrm{z}-3-\left.2 \mathrm{i}\right|^{2}=8\right\}$
$\mathrm{S}_{2}=\{\mathrm{z} \in \mathrm{C} \mid \operatorname{Re}(\mathrm{z}) \geq 5\}$ and
$\mathrm{S}_{3}=\{\mathrm{z} \in \mathrm{C}|| \mathrm{z}-\overline{\mathrm{z}} \mid \geq 8\}$
Then the number of elements in $S_{1} \cap S_{2} \cap S_{3}$ is equal to
Correct Option: 1
$\mathrm{S}_{1}:|\mathrm{z}-3-2 \mathrm{i}|^{2}=8$
$|z-3-2 i|=2 \sqrt{2}$
$(x-3)^{2}+(y-2)^{2}=(2 \sqrt{2})^{2}$
$\mathrm{S}_{2}: \mathrm{x} \geq 5$
$\mathrm{S}_{3}:|\mathrm{z}-\overline{\mathrm{z}}| \geq 8$
$|2 \mathrm{iy}| \geq 8$
$2|\mathrm{y}| \geq 8 \quad \therefore \mathrm{y} \geq 4, \mathrm{y} \leq-4$
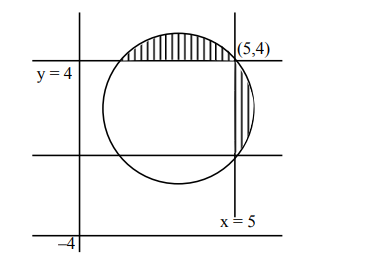
$\mathrm{n}\left(\mathrm{S}_{1} \cap \mathrm{S}_{2} \cap \mathrm{S}_{3}\right)=1$
