Question:
Let $\mathrm{f}:[-3,1] \rightarrow \mathrm{R}$ be given as
$f(x)= \begin{cases}\min \left\{(x+6), x^{2}\right\}, & -3 \leq x \leq 0 \\ \max \left\{\sqrt{x}, x^{2}\right\}, & 0 \leq x \leq 1\end{cases}$
If the area bounded by $y=f(x)$ and $x$-axis is $\mathrm{A}$, then the value of $6 \mathrm{~A}$ is equal to
Solution:
$\mathrm{f}:[-3,1] \rightarrow \mathrm{R}$
$f(x)= \begin{cases}\min \left\{(x+6), x^{2}\right\} & ,-3 \leq x \leq 0 \\ \max \left\{\sqrt{x}, x^{2}\right\} & , 0 \leq x \leq 1\end{cases}$
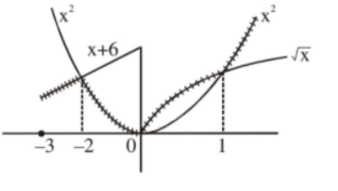
area bounded by $y=f(x)$ and $x$-axis
$=\int_{-3}^{-2}(x+6) \mathrm{d} x+\int_{-2}^{0} x^{2} d x+\int_{0}^{1} \sqrt{x} d x$
$A=\frac{41}{6}$
$6 \mathrm{~A}=41$
