Question:
Let $B$ be the centre of the circle $x^{2}+y^{2}-2 x+4 y+1=0$. Let the tangents at two points $\mathrm{P}$ and $\mathrm{Q}$ on the circle
Solution:
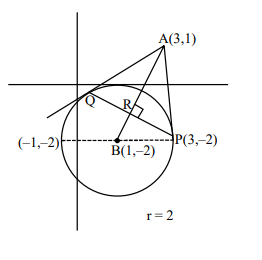
$\tan \theta=\frac{3}{2}$
$\frac{\text { Area } \Delta \mathrm{APQ}}{\text { Area } \Delta \mathrm{BPQ}}=\frac{\mathrm{AR}}{\mathrm{RB}}=\frac{3 \sin \theta}{2 \cos \theta}=\frac{9}{4}$
$8\left(\frac{\text { Area } \triangle \mathrm{APQ}}{\text { Area } \triangle \mathrm{BPQ}}\right)=18$
