Question:
Let a function $\mathrm{g}:[0,4] \rightarrow \mathbf{R}$ be defined as
$g(x)= \begin{cases}\max _{0 \leq t \leq x}\left\{t^{3}-6 t^{2}+9 t-3\right\}, & 0 \leq x \leq 3 \\ 4-x & , 3 then the number of points in the interval $(0,4)$ where $g(x)$ is NOT differentiable, is
Solution:
$f(x)=x^{3}-6 x^{2}+9 x-3$
$f^{\prime}(x)=3 x^{2}-12 x+9=3(x-1)(x-3)$
$f(1)=1 \mathrm{f}(3)=-3$
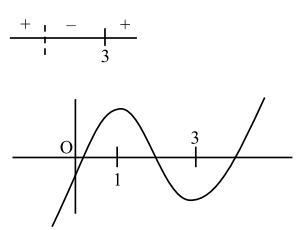
$g(x)=\left[\begin{array}{rr}f(x) & 0 \leq x \leq 1 \\ 0 & 1 \leq x \leq 3 \\ -1 & 3 $\mathrm{g}(\mathrm{x})$ is continuous $g^{\prime}(x)=\left[\begin{array}{cc}3(x-1)(x-3) & 0 \leq x \leq 1 \\ 0 & 1 \leq x \leq 3 \\ -1 & 3 $\mathrm{g}(\mathrm{x})$ is non-differentiable at $\mathrm{x}=3$
