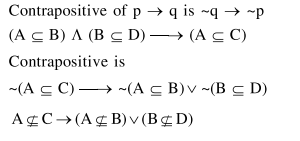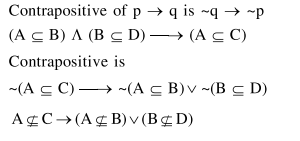Question: Let $\mathrm{A}, \mathrm{B}, \mathrm{C}$ and $\mathrm{D}$ be four non-empty sets. The contrapositive statement of "If $\mathrm{A} \subseteq \mathrm{B}$ and $\mathrm{B} \subseteq \mathrm{D}$, then $\mathrm{A} \subseteq \mathrm{C}^{\prime \prime}$ is :
If $\mathrm{A} \subseteq \mathrm{C}$, then $\mathrm{B} \subset \mathrm{A}$ or $\mathrm{D} \subset \mathrm{B}$
If $\mathrm{A} \nsubseteq \subseteq \mathrm{C}$, then $\mathrm{A} \nsubseteq \subseteq \mathrm{B}$ or $\mathrm{B} \not \subseteq \mathrm{D}$
If $\mathrm{A} \nsubseteq \subseteq \mathrm{C}$, then $\mathrm{A} \subseteq \mathrm{B}$ and $\mathrm{B} \subseteq \mathrm{D}$
If $\mathrm{A} \nsubseteq \mathrm{C}$, then $\mathrm{A} \nsubseteq \mathrm{B}$ and $\mathrm{B} \subseteq \mathrm{D}$
Correct Option: , 2
Solution: