Let $A_{1} A_{2} A_{3} A_{4} A_{5} A_{6} A_{1}$ be a regular hexagon. Write the x-components of the vectors represented by the six sides taken in order. Use the fact that the resultant of these six vectors is zero, to prove that $\cos 0+\cos \pi / 3+\cos 2 \pi / 3+\cos 4 \pi / 3+\cos 5 \pi / 3=0$
Use the known cosine values to verify the result.
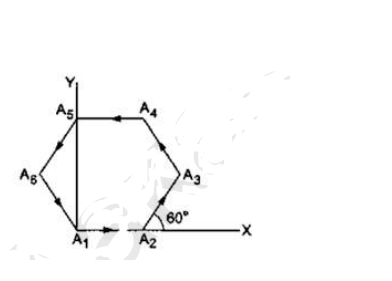
From polygon law of vector addition, the resultant of the six vectors can be affirmed to be zero. Here their magnitudes are the same.
That is, $\mathrm{A}=\mathrm{B}=\mathrm{C}=\mathrm{D}=\mathrm{E}=\mathrm{F}$.
$R x=A \cos \rightarrow+A \cos \Rightarrow / 3+A \cos 2 \Rightarrow / 3+A \cos 3 \Rightarrow / 3+A \cos$
$4 \Rightarrow / 4+A \cos 5 \Rightarrow / 5=0$ [As resultant is zero, $x$ component of
resultant is also 0]
Now taking $\mathrm{A}$ common and putting $\mathrm{Rx}=0$,
$\cos \Rightarrow+\cos \Rightarrow / 3+\cos 2 \Rightarrow / 3+\cos 3 \Rightarrow / 3+\cos 4 \Rightarrow / 3+\cos 5 \Rightarrow / 3=0$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.