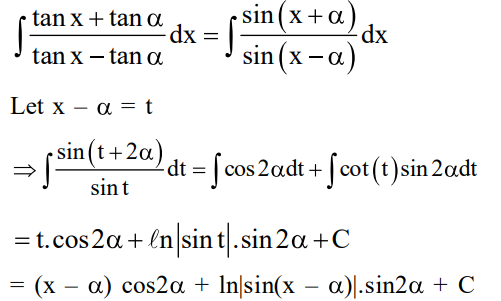Question:
Let $\alpha \in(0, \pi / 2)$ be fixed. If the integral
$\int \frac{\tan x+\tan \alpha}{\tan x-\tan \alpha} d x=$
$A(x) \cos 2 \alpha+B(x) \sin 2 \alpha+C$, where $C$ is a constant of integration, then the functions $A(x)$ and $B(x)$ are respectively :
Correct Option: , 3
Solution: