Question:
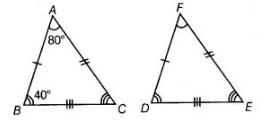
It is given that ΔABC = ΔFDE and AB = 5 cm, ∠B = 40° and ∠A = 80°, then Which of the following is true?
(a) DF = 5 cm, ∠F = 60°
(b) DF = 5 cm, ∠E =60°
(c) DE = 5 cm, ∠E = 60°
(d) DE = 5 cm, ∠D = 40°
Solution:
(b) Given, $\triangle A B C \cong \triangle F D E$ and $A B=5 \mathrm{~cm}, \angle B=40^{\circ}, \angle A=80^{\circ}$
Since, $\triangle F D E \cong \triangle A B C$
$\therefore \quad D F=A B$ [by CPCT]
$D F=5 \mathrm{~cm}$
and $\angle E=\angle C$ [by CPCT]
$\Rightarrow \quad \angle E=\angle C=180^{\circ}-(\angle A+\angle B)$
[by angle sum property of a $\triangle A B C$ ]
$\Rightarrow \quad \angle E=180^{\circ}-\left(80^{\circ}+40^{\circ}\right)$
$\Rightarrow \quad \angle E=60^{\circ}$
