In two concentric circles, a chord of length 8 cm of the larger circle touches the smaller circle.

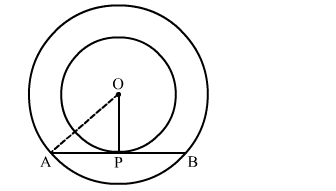
We know that the radius and tangent are perperpendular at their point of contact
Since, the perpendicular drawn from the centre bisect the chord.

$\therefore \mathrm{AP}=\mathrm{PB}=\frac{\mathrm{AB}}{2}=4 \mathrm{~cm}$

In right  triangle AOP
AO2 = OP2 + PA2
⇒ 52 = OP2 + 42
⇒ OP2 = 9
⇒ OP = 3 cm
Hence, the radius of the smaller circle is 3 cm.