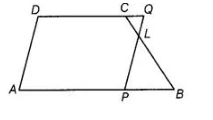
In trapezium ABCD, AB || DC and L is the mid-point of BC.

Solution:

Given in trapezium $A B C D, A B \| D C, D C$ produced in $Q$ and $L$ is the mid-point of $B C$.

$\therefore \quad B L=C L$

To prove $\operatorname{ar}(A B C D)=\operatorname{ar}(A P Q D)$

Proof Since, $D C$ produced in $Q$ and $A B \| D C$.

So, $D Q \| A B$

In $\triangle C L Q$ and $\triangle B L P$,

$C L=B L$ [since, $L$ is the mid-point of $B C$ ]

$\angle L C Q=\angle L B P$ [alternate interior angles as $B C$ is a transversal]

$\angle C Q L=\angle L P B$ [alternate interior angles as $P Q$ is a transversal]

$\therefore \quad \triangle C L Q \cong \triangle B L P \quad$ [by AAS congruence rule]

Then, $\operatorname{ar}(\Delta C L Q)=\operatorname{ar}(\Delta B L P)$ $\ldots(i)$

[since, congruent triangles have equal area]

Now, $\quad \operatorname{ar}(A B C D)=\operatorname{ar}(A P Q D)-\operatorname{ar}(\Delta C Q L)+\operatorname{ar}(\triangle B L P)$

$=\operatorname{ar}(A P Q D)-\operatorname{ar}(\Delta B L P)+\operatorname{ar}(\Delta B L P) \quad$ [from Eq. (1)]

$\Rightarrow \quad a r(A B C D)=\operatorname{ar}(A P Q D)$ 

Hence proved.