In the middle of a rectangular field measuring 30m × 20m, a well of 7 m diameter and 10 m depth is dug.
Question:
In the middle of a rectangular field measuring 30m × 20m, a well of 7 m diameter and 10 m depth is dug. The earth so removed is evenly spread over the remaining part of the field. Find the height through which the level of the field is raised.
Solution:
Let r m be the radius and h m be the depth of the well that is dug.
Volume of the well $=\pi r^{2} h=$$\frac{22}{7}$× (3.5 m)2 × (10 m) = 385 m3
Volume of the well = Volume of the rectangular field
Volume of the rectangular field = 385 m3 = 30 m × 20 m × height
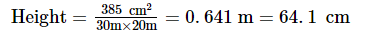
Hence, the height through which the level of the field is raised is 64.1 cm.
