Question:
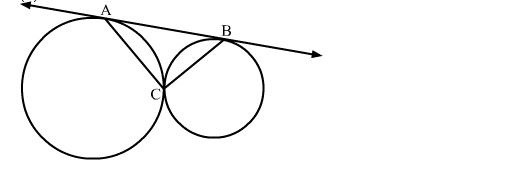
In the given figure, two circles touch each other at C and AB is a tangent to both the circles. The measure of ∠ACB is
(a) 45∘
(b) 60∘
(c) 90∘
(d) 120∘
Solution:
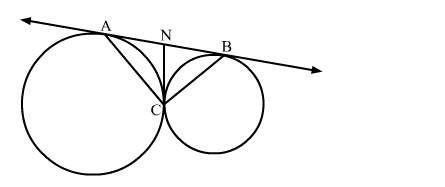
We know that tangent segments to a circle from the same external point are congruent.
Therefore, we have
NA = NC and NC = NB
We also know that angle opposite to equal sides are equal
∴ ∠NAC = ∠NCA and ∠NBC = ∠NCB
Now, ∠ANC + ∠BNC = 180∘ [Linear pair angles]
⇒ ∠NBC + ∠NCB + ∠NAC + ∠NCA= 180∘ [Exterior angle property]
⇒ 2∠NCB + 2∠NCA= 180∘
⇒ 2(∠NCB + ∠NCA) = 180∘
⇒ ∠ACB = 90∘
Hence, the correct answer is option (c).
