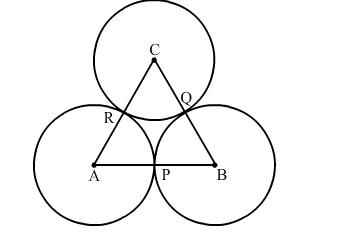
In the given figure, three circles with centres A, B, C, respectively,

(b) 2 cm

Given, $A B=5 \mathrm{~cm}, B C=7 \mathrm{~cm}$ and $C A=6 \mathrm{~cm}$.

Let, $A R=A P=x \mathrm{~cm}$.

$B Q=B P=y \mathrm{~cm}$

$C R=C Q=z \mathrm{~cm}$

(Since the length of tangents drawn from an external point are equal)

Then, $A B=5 \mathrm{~cm}$

$\Rightarrow A P+P B=5 \mathrm{~cm}$

$\Rightarrow x+y=5 \ldots \ldots(i)$

Similarly, $y+z=7 \ldots \ldots \ldots($ (ii)

and $z+x=6 \ldots(i i i)$

Adding (i), (ii) and (iii), we get:

$(x+y)+(y+z)+(z+x)=18$

$\Rightarrow(x+y+z)=9 \ldots \ldots .(i v)$

Now, $(i v)-(i i):$

$(x+y+z)-(y+z)=(9-7)$

$\Rightarrow x=2$

$\therefore$ The radius of the circle with centre A is $2 \mathrm{~cm}$.