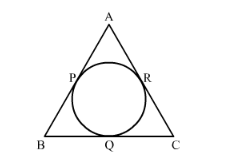
In the given figure, the sides AB ,

It is given that the sides AB , BC and CA of ∆ABC touch a circle at P, Q and R, respectively.

Also, PA = 4 cm, PB = 3 cm and AC = 11 cm

We know that, the lengths of tangents drawn from an external point to a circle are equal.

∴ AR = AP = 4 cm

BQ = BP = 3 cm

Now, CR = AC − AR = 11 cm − 4 cm = 7 cm

∴ CQ = CR = 7 cm         (Lengths of tangents drawn from an external point to a circle are equal)

Now,

BC = BQ + CQ = 3 cm + 7 cm = 10 cm

Thus, the length of BC is 10 cm.

Hence, the correct answer is option B.